Motivation
As models usually learn “too well” during training - so much that make various types of attacks possible, backdoor attack (or Trojan Attack) has become a real-life threat to the AI model deployed in the real world. At the same time, extensive research work on model pruning has shown that the weights of an overparameterized model (e.g., DNN) can be pruned without hampering its generalization ability. Combining both lines of research, our story begins with the following question:
The Discovery of ‘Winning Trojan Ticket’
Trojan features learned by backdoored attacks are significantly more stable against pruning than benign features. Therefore, Trojan attacks can be uncovered through the pruning dynamics of the Trojan model.
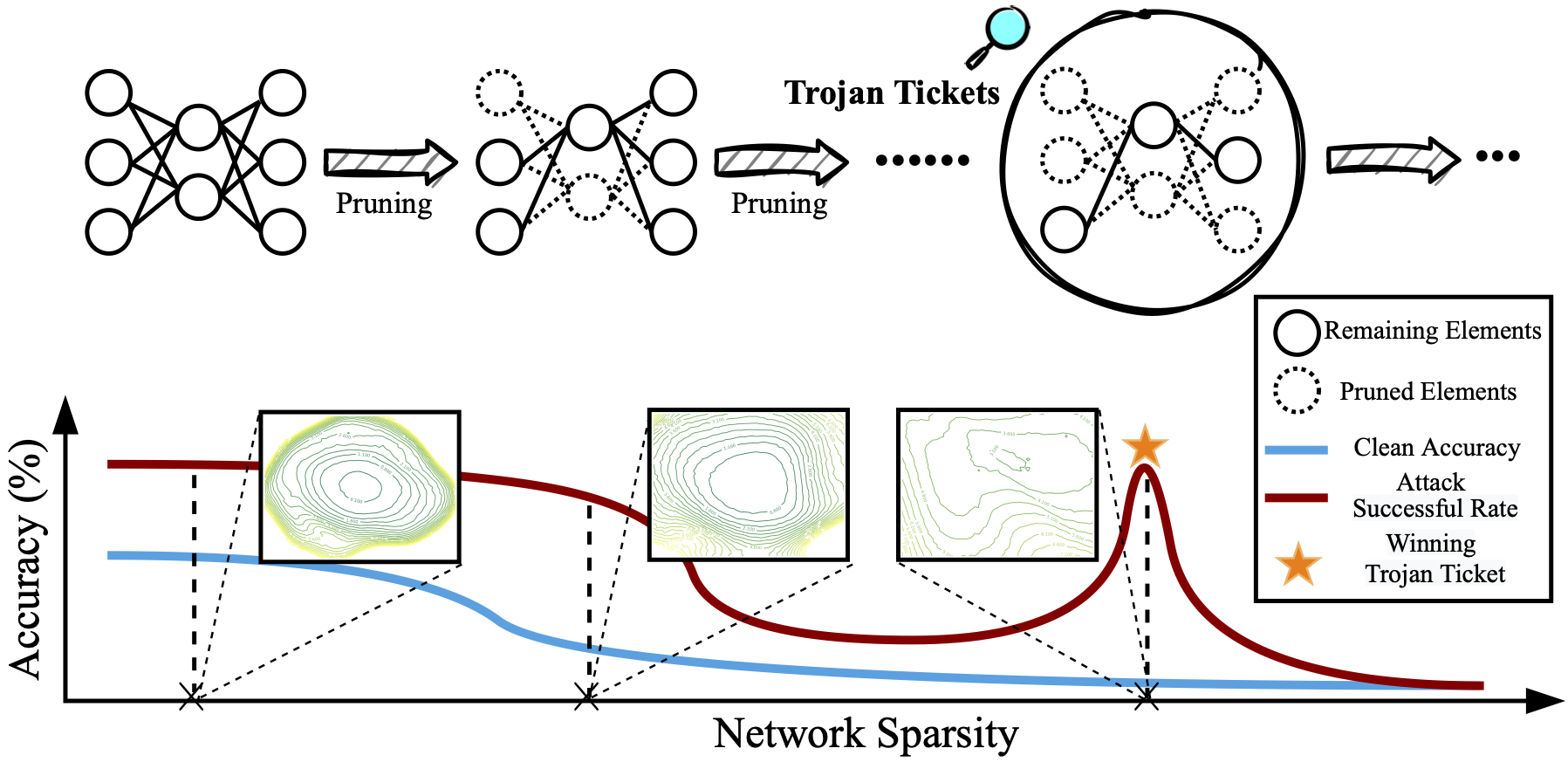
Leveraging LTH-oriented iterative magnitude pruning (IMP), the ‘winning Trojan Ticket’ can be discovered, which preserves the Trojan attack performance while retaining chance-level performance on clean inputs.
Thus, the existence of the ‘winning Trojan Ticket’ could serve as an indicator of Trojan attacks. However, in real-world applications, it is hard for the users to acquire the ASR (namely the red curve in Figure 1), as the attack information is transparent to the users. Thus, we need to find a substitute indicator for ASR, which does not require any attack information or even clean data.
The winning Trojan ticket can be detected by our proposed linear model connectivity (LMC)-based Trojan score.
Trojan Score: Linear Mode Connectivity-based Trojan Indicator
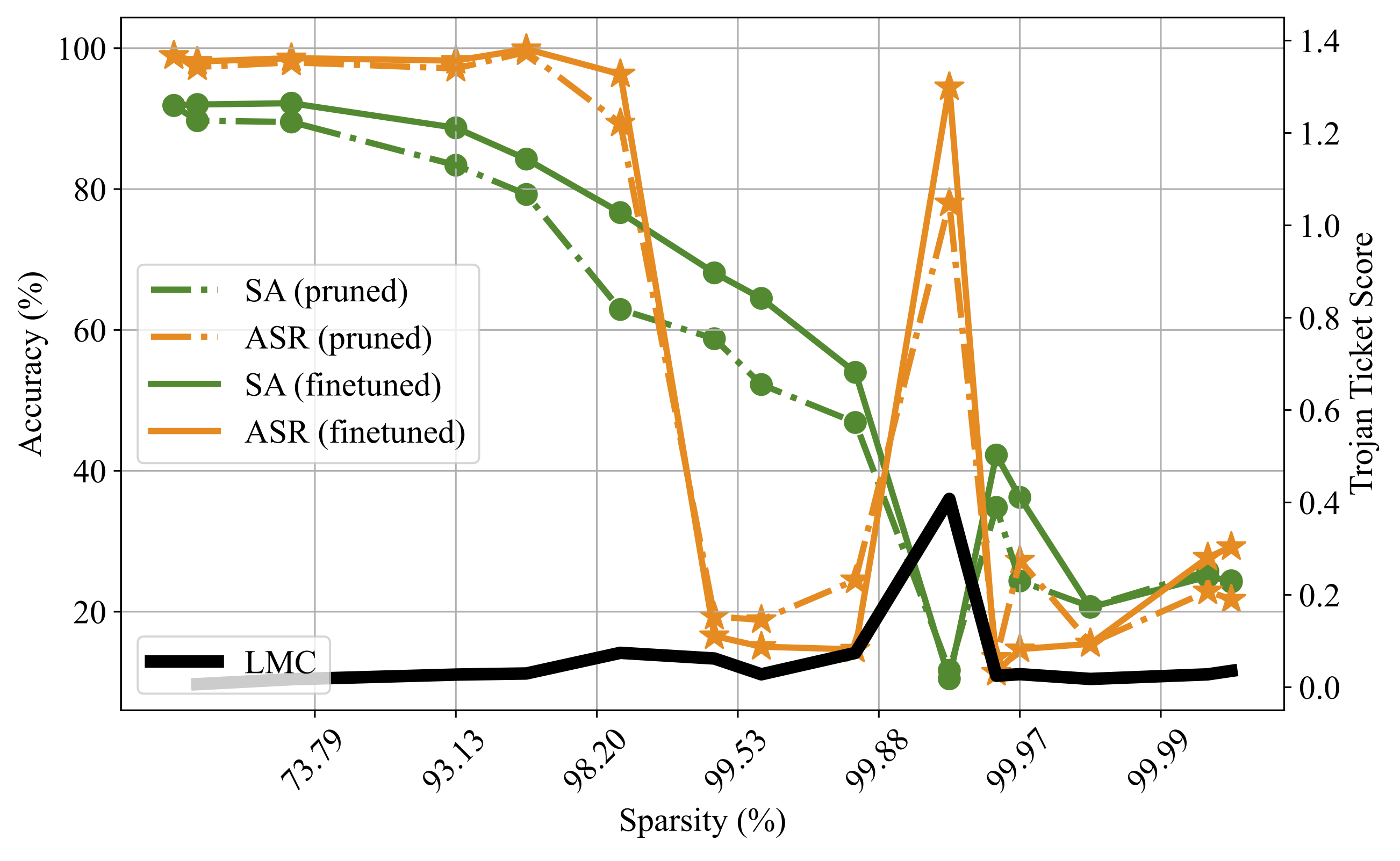
We adopt Linear Mode Connectivity [2] (LMC) to measure the stability of the Trojan ticket ϕ:=(m⊙θ) v.s. the k-step finetuned Trojan ticket ϕ:=(m⊙θ(k)).
We define the Trojan Score as
STrojan=maxα∈[0,1]E(αϕ−(1−α)ϕk)−ϕ−ϕk2where the first term denotes LMC and the second term an error baseline. E(ϕ) denotes the training error of the model ϕ.
A sparse network with the peak Trojan Score maintains the highest ASR in the extreme pruning regime and is termed as the Winning Trojan Ticket.
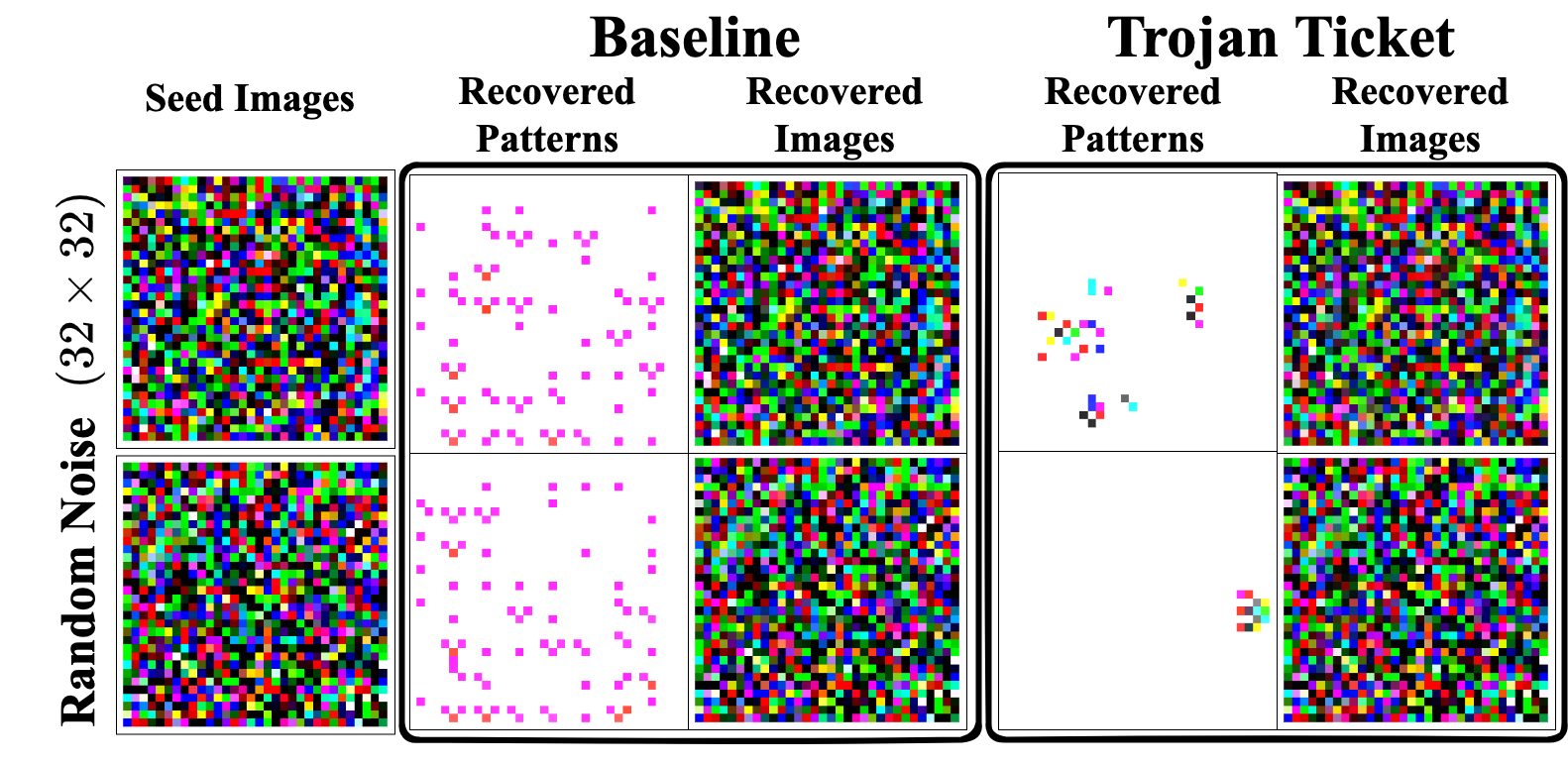
Backdoor Trigger Reverse Engineering
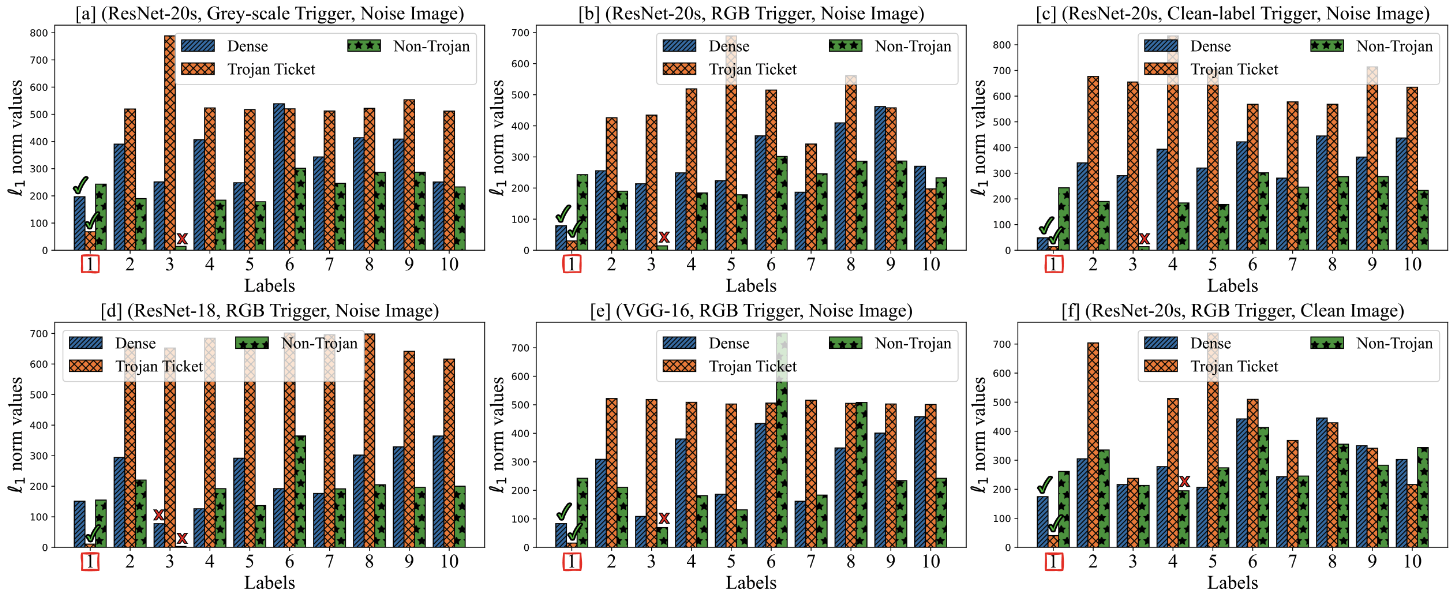
Trigger Reverse Engineer
Citation
@inproceedings{chen2022quarantine,
title = {Quarantine: Sparsity Can Uncover the Trojan Attack Trigger for Free},
author = {Chen, Tianlong and Zhang, Zhenyu and Zhang, Yihua and Chang, Shiyu and Liu, Sijia and Wang, Zhangyang},
booktitle = {Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition},
pages = {598--609},
year = {2022}
}
Reference
[1] Jonathan Frankle et al. “The Lottery Ticket Hypothesis: Finding Sparse, Trainable Neural Networks.” ICLR 2019.
[2] Jonathan Frankle et al. “Linear Mode Connectivity and the Lottery Ticket Hypothesis.” ICML 2020.
[3] Ren Wang et al. “Practical detection of trojan neural networks: Data-limited and data-free cases.” ECCV 2020.