[ICLR24] DeepZero: Scaling up Zeroth-Order Optimization for Deep Model Training

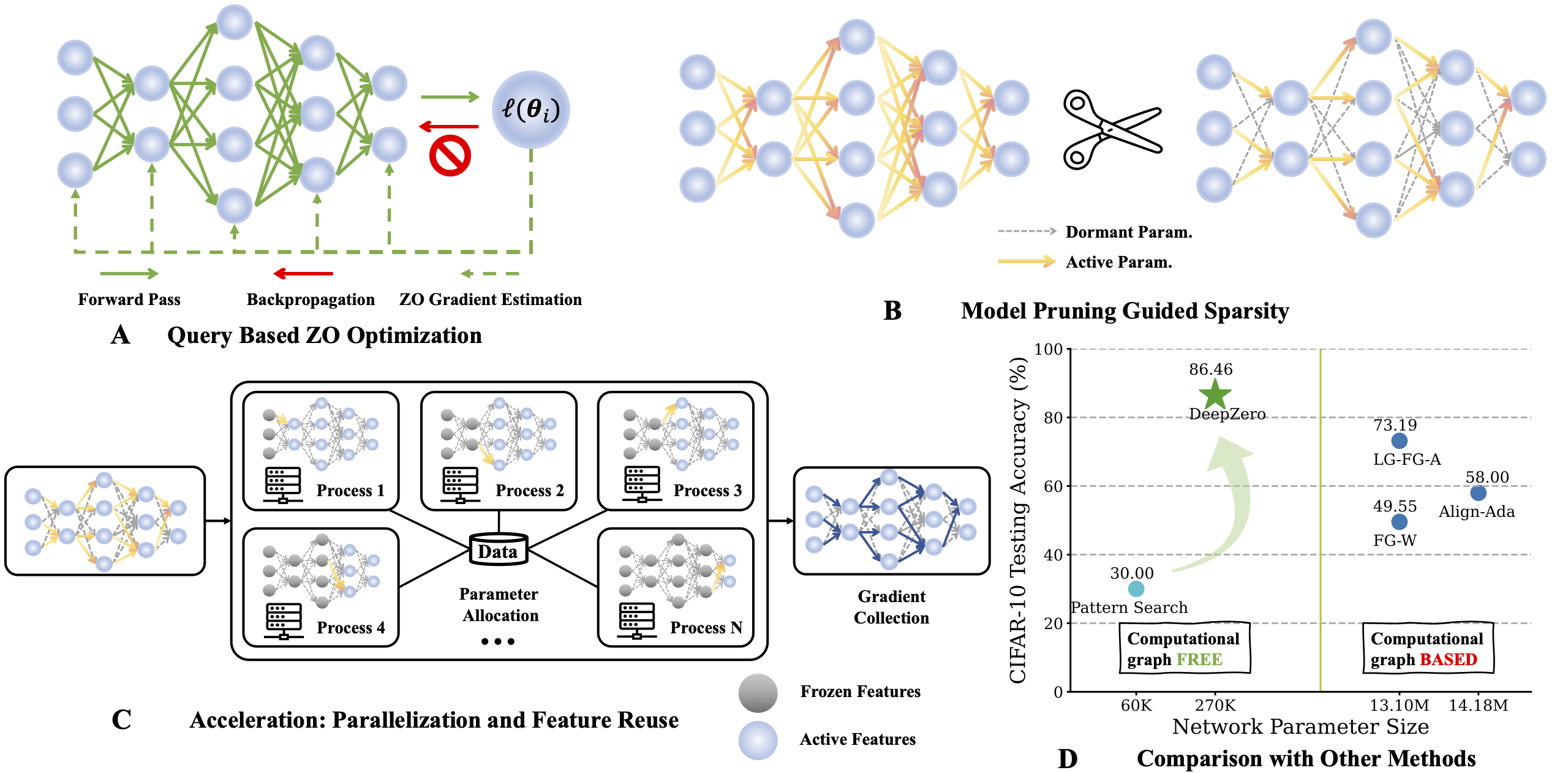
Overview of DeepZero, a principled ZO deep learning (DL) framework that can scale ZO optimization to DNN training from scratch.

Motivations: Why Zeroth-Order (ZO) Optimization needed for model training?

Zeroth-order (ZO) optimization has become a popular technique for solving machine learning (ML) problems when first-order (FO) information is difficult or impossible to obtain:

1. Disciplines like physics and chemistry: ML models may interact with intricate simulators or experiments where the underlying systems are non-differentiable.

2. Black-box learning scenarios: When deep learning (DL) models are integrated with third-party APIs, such as adversarial attack and defense against black-box DL models and black-box prompt learning for language-model-as-a-service.

3. Limited hardware: The principled backpropagation (BP) mechanism for calculating FO gradients may also not be supported when implementing DL models on hardware systems.

However, the scalability of ZO optimization remains an open problem: Its use has primarily been limited to relatively small-scale ML problems, such as sample-wise adversarial attack generation. As problem dimensionality increases, the accuracy and efficiency of traditional ZO methods deteriorate. This is because ZO finite difference-based gradient estimates are biased estimators of FO gradients, and the bias becomes more pronounced in higher-dimensional spaces. These challenges motivate the central question addressed in this work:

How to scale up ZO optimization for training deep models ?

ZO Gradient Estimator: RGE or CGE?

The ZO optimizer interacts with the objective function \(\ell\) only by submitting inputs (i.e., realizations of \(\boldsymbol \theta\)) and receiving the corresponding function values. There are two main ZO gradient estimation schemes: deterministic coordinate-wise gradient estimation (CGE) and randomized vector-wise gradient estimation (RGE) as shown below:

where \(\hat{\nabla}_{\boldsymbol \theta} \ell\) denotes an estimation of the FO gradient \(\nabla_{\boldsymbol \theta}\ell\) with respect to optimization variables \(\boldsymbol \theta \in \mathbb R^d\) (e.g., model parameters of a neural network).

In (RGE), \(\mathbf u_i\) denotes a randomized perturbation vector, e.g., drawn from the standard Gaussian distribution \(\mathcal N(\mathbf 0, \mathbf I)\), \(\mu > 0\) is a perturbation size (a.k.a. smoothing parameter), and \(q\) is the number of random directions used to acquire finite differences.

In (CGE), \(\mathbf e_i\) denotes a standard basis vector, and \(\frac{\ell(\boldsymbol \theta + \mu \mathbf e_i) - \ell(\boldsymbol \theta)}{\mu}\) provides the finite-difference estimation of the partial derivative of \(\ell(\boldsymbol \theta)\) at the \(i\)th coordinate \(\boldsymbol \theta_i\).

Compared to CGE, RGE has the flexibility to specify \(q < d\) to reduce the number of function evaluations. Despite the query efficiency, it remains uncertain whether RGE can deliver satisfactory accuracy when training a deep model from scratch. To this end, we undertake a preliminary investigation wherein we train a basic convolutional neural network (CNN) of different sizes on CIFAR-10, employing both RGE and CGE. As the two figures below show, CGE can achieve test accuracy comparable to FO training and significantly outperforms RGE and also greater time efficiency than RGE.

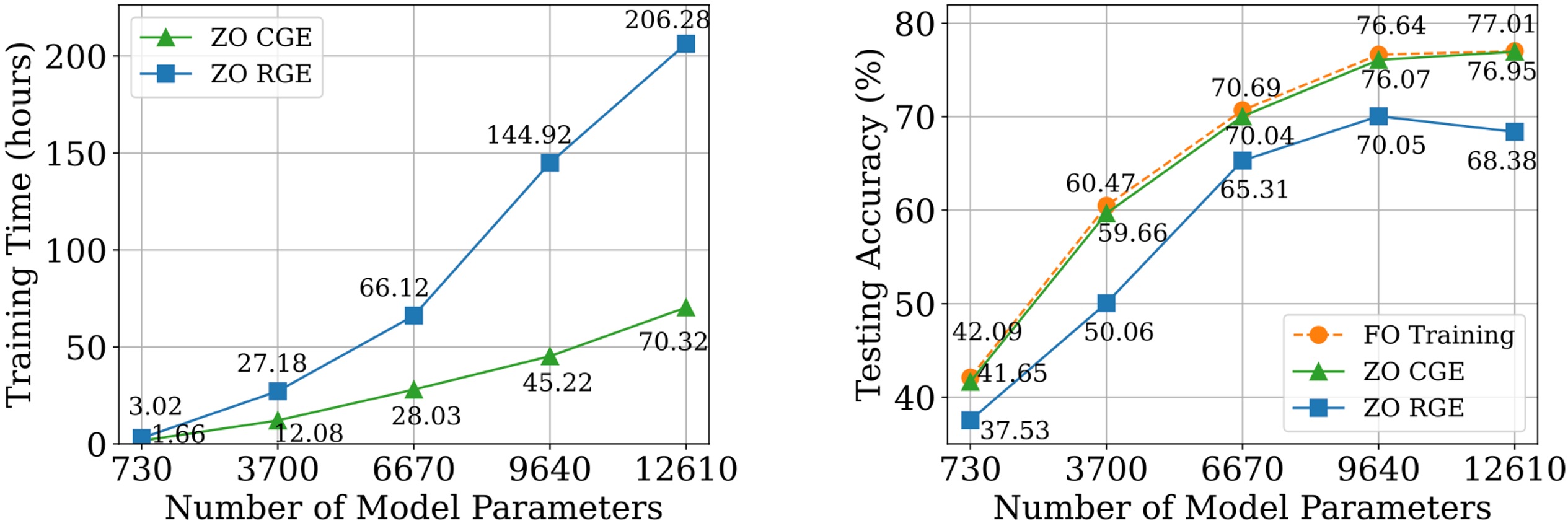
Based on the advantages of CGE over RGE in terms of both accuracy and computation efficiency, we choose CGE as the preferred ZO gradient estimator. However, query complexity of CGE is still a bottleneck, as it scales with model size \(d\).

Proposed ZO DL Framework: DeepZero

To our best knowledge, no prior work has demonstrated the effectiveness of ZO optimization in training deep neural networks (DNNs) without a significant decrease in performance. To overcome this roadblock, we develop DeepZero, a principled ZO deep learning (DL) framework that can scale ZO optimization to DNN training from scratch.

1. Model pruning via ZO oracle: ZO-GraSP: A randomly initialized, dense neural network contains a high-quality sparse subnetwork. However, most effective pruning methods incorporate model training as an intermediate step. Thus, they are not well-suited for finding sparsity via a ZO oracle.To address the above challenge, we draw inspiration from training-free pruning methods, known as pruning-at-initialization. Within this family, gradient signal preservation (GraSP) is a method to identify the sparsity prior of DL through the gradient flows of a randomly-initialized network.

2. Sparse Gradient: To retain the accuracy benefits of training dense models, we incorporate gradient sparsity (in CGE) rather than weight sparsity. This ensures that we train a dense model in the weight space, rather than training a sparse model. Specifically, we leverage ZO-GraSP to determine layer-wise pruning ratios (LPRs) that can capture DNN compressibility and then ZO optimization can train the dense model by iteratively updating partial model parameter weight with their corresponding gradient estimation by CGE, where the sparse gradient ratio determined by LPRs.

3. Feature Reuse: Since CGE perturbs each parameter element-wise, it can reuse the feature immediately preceding the perturbed layer and carry out the remaining forward pass operations instead of starting from the input layer. Empirically, CGE with feature reuse exhibits a 2X reduction in training time.

4. Forward Parallelization: CGE enables parallelization of model training due to its alignment of parameter perturbations with forward passes. The decoupling property enables scaling forward passes via distributed machines, which can significantly improve ZO training speed.

Performance Comparison

Image classification

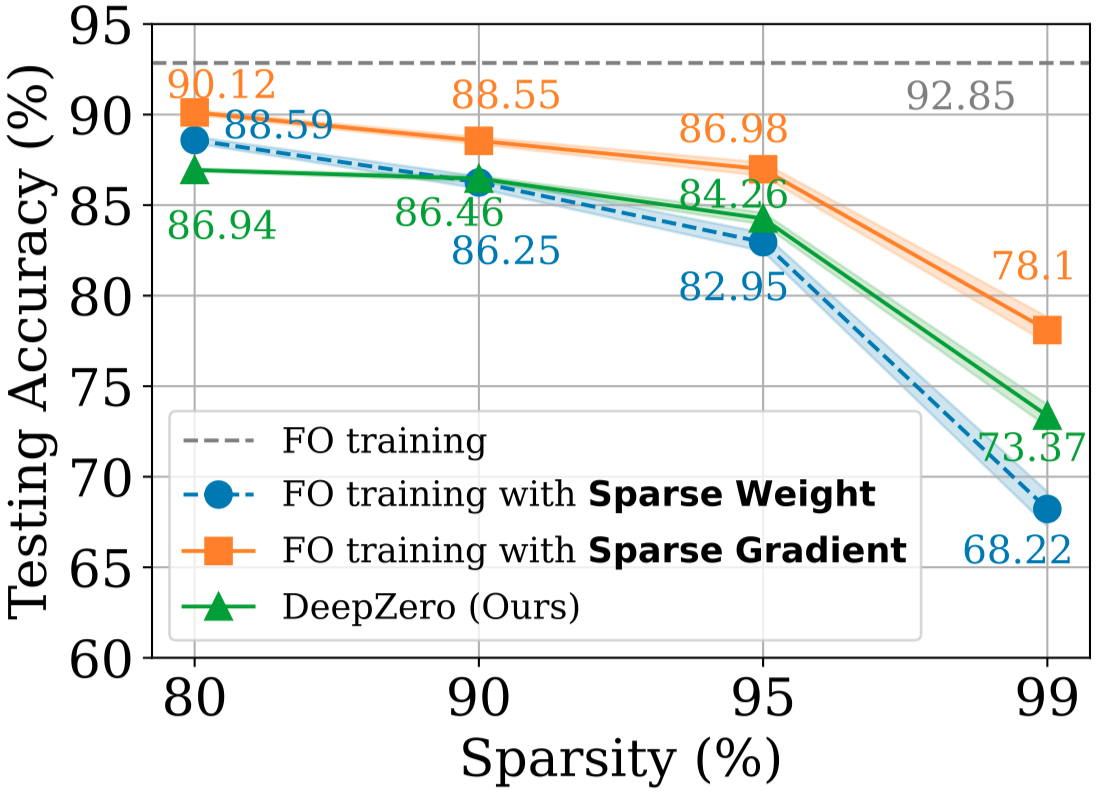
we compare the accuracy of DeepZero-trained ResNet-20 with two variants trained by FO recipes:

• (1) a dense ResNet-20 acquired through FO training
• (2) a sparse ResNet20 acquired through FO training under FO-GraSP sparsity pattern.

As shown in figure below, the accuracy gap still exists between (1) and the model trained with DeepZero in the sparsity regime of 80% to 99%. This highlights the challenge of ZO optimization for deep model training, where achieving high sparsity is desired to reduce the number of model queries in Sparse CGE for scaling to ResNet-20. Notably, in the sparsity regime of 90% to 99%, DeepZero outperforms (2), showcasing the superiority of gradient sparsity in DeepZero compared to weight sparsity (i.e., directly training a sparse model).

Black-box defense

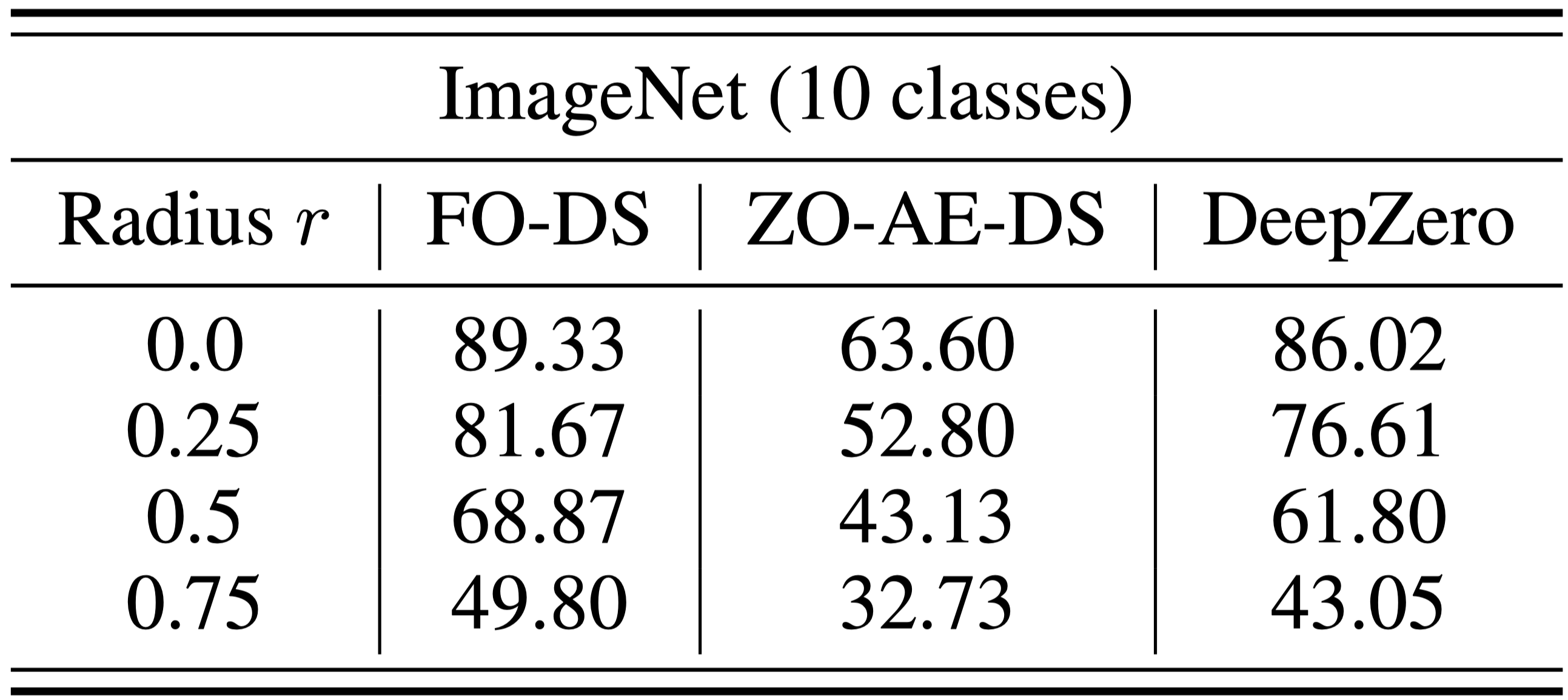
The black-box defense problem arises when the owner of an ML model is unwilling to share the model details with the defender against adversarial attacks. This poses a challenge for existing robustness enhancement algorithms that directly robustify white-box ML models using FO training. To overcome this challenge, ZO-AE-DS [1] are proposed to introduces an autoencoder (AE) between the white-box denoised smoothing (DS) defense operation (to be learned) and the black-box image classifier to address dimensionality challenges with ZO training. The downside of ZO-AE-DS is poor scaling to high-resolution datasets (e.g., ImageNet) due to the use of AE, which compromises the fidelity of the image input to the black-box image classifier and leads to inferior defense performance. In contrast, DeepZero can directly learn the defense operation integrated with the black-box classifier, without needing AE. As shown in table below, DeepZero consistently outperforms ZO-AE-DS in terms of certified accuracy (CA) for all values of input perturbation radius \(r > 0\).

Simulation-coupled DL

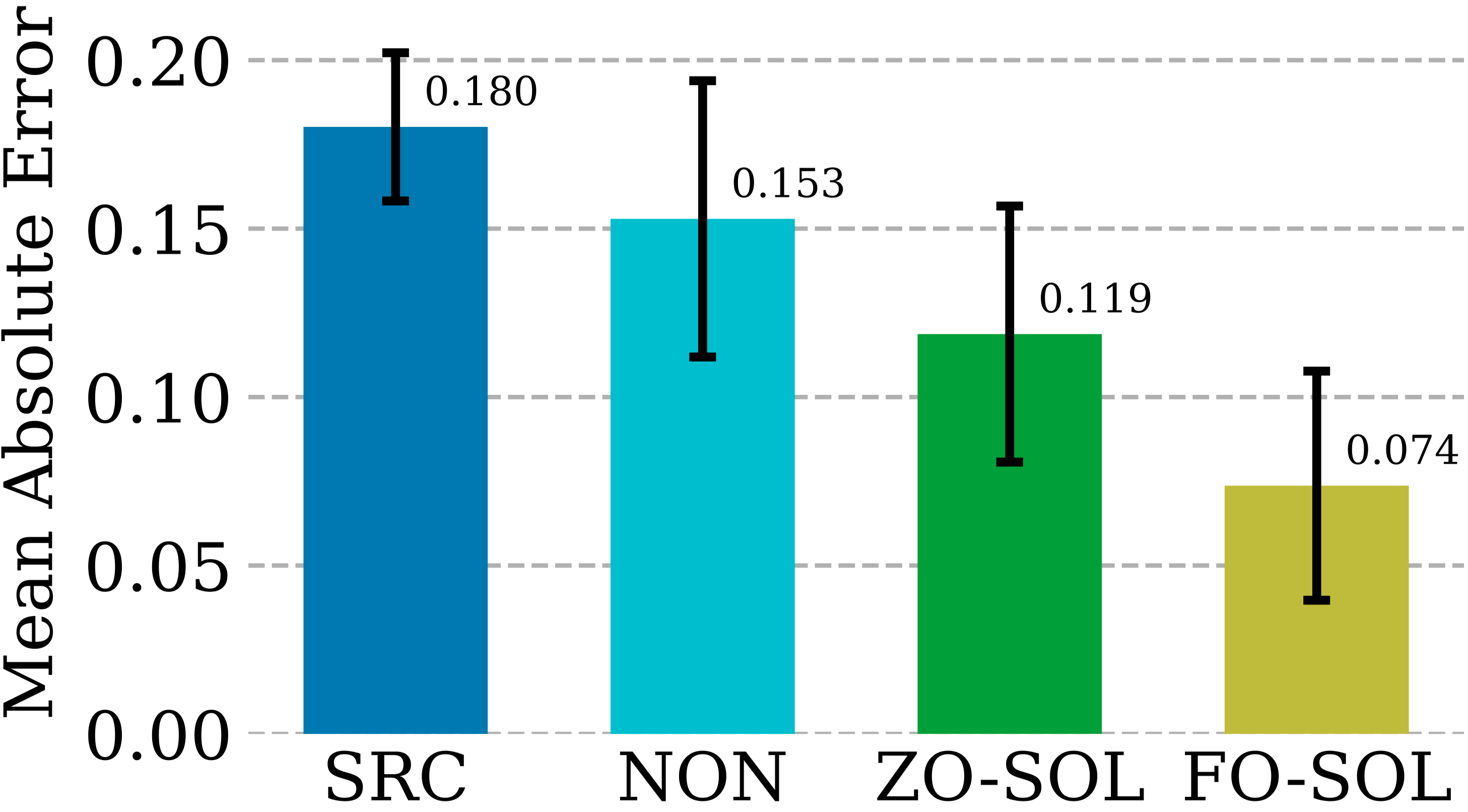
Numerical methods, while instrumental in providing physics-informed simulations, come with their own challenge: the discretization unavoidably produces numerical errors. The feasibility of training a corrective neural network through looping interactions with the iterative partial differential equation (PDE) solver, coined ‘solver-in-the-loop’ (SOL) [2]. While existing work focused on using or developing differentiable simulators for model training, we extend SOL by leveraging DeepZero, enabling its use with non-differentiable or blackbox simulators. The table below compares the test error correction performance of ZO-SOL (via DeepZero) with three differentiable approaches methods:

• SRC (low fidelity simulation without error correction),
• NON (non-interactive training out of the simulation loop using pre-generated low and high fidelity simulation data),
• FO-SOL (FO training for SOL given a differentiable simulator).

The error for each test simulation is computed as the mean absolute error (MAE) of the corrected simulation compared to the high fidelity simulation averaged across all simulation timesteps. The results demonstrate that ZO-SOL achieved by DeepZero outperforms the SRC and NON baselines, and narrows the performance gap with FO-SOL, despite only having query-based access to the simulator. Comparing ZO-SOL with NON highlights the promise of ZO-SOL even when integrated with black-box simulators.

Citation

@article{chen2023deepzero,
  title={DeepZero: Scaling up Zeroth-Order Optimization for Deep Model Training},
  author={Chen, Aochuan and Zhang, Yimeng and Jia, Jinghan and Diffenderfer, James and Liu, Jiancheng and Parasyris, Konstantinos and Zhang, Yihua and Zhang, Zheng and Kailkhura, Bhavya and Liu, Sijia},
  journal={arXiv preprint arXiv:2310.02025},
  year={2023}
}

References

[1] Zhang et al. (ICLR 2022). How to robustify black-box ml models? a zeroth-order optimization perspective

[2] Um et al. (NeurIPS 2020). Solver-in-the-loop: Learning from differentiable physics to interact with iterative pde-solvers.